Разработчик
Скриптер
Проверенный
Участник
Пользователь
- Сообщения
- 273
- Реакции
- 424
- Помог
- 5 раз(а)
Ниже представлена заключительная часть перевода документа Stefan Hajnoczi (оригинал документа и исходные коды на GitHub).
Далее я создам тему посвящённую этим статьям, где планирую выложить их в виде одного файла, а так же некоторые свои решения по оптимизации кода.
Сортировка вершин
Теперь у нас есть список допустимых полигонов с координатами текстуры для каждой вершины, мы уже довольно далеко продвинулись. Однако наши вершины расположены в более или менее случайном порядке. Чтобы воспользоваться преимуществами алгоритма отбраковки задних граней, вершины каждого полигона должны быть отсортированы либо по часовой стрелке, либо против часовой стрелки. Я предпочитаю сортировку по часовой стрелке, чтобы можно было отбраковывать полигоны с вершинами, расположенными против часовой стрелки. Описываемый мной метод также можно использовать с небольшими изменениями для сортировки вершин в порядке против часовой стрелки. Чтобы отсортировать вершины, нам нужна нормаль полигона. Но она у нас уже есть, и это нормаль грани, на плоскости которой лежит полигон.
Для начала нам нужно найти центр полигона. Это не что иное, как среднее значение всех его вершин. Псевдокод вычисления центра полигона:
Используя центр полигона в качестве ориентира, мы можем найти вершину с наименьшим углом к текущей вершине. Это мы проделываем до предпоследней вершины. Вот диаграмма того, что мы пытаемся найти:
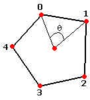
O это наименьший угол. Вершина с наименьшим углом к вершине 1 - это вершина 2. Вершина с наименьшим углом к вершине 2 - это вершина 3. Теперь наш отсортированный список вершин должен быть 0, 1, 2, 3. Осталась только вершина 4, поэтому она должна быть последней.
Хотя это легко понять,но как мы можем сделать это математически? Для поиска угла между векторами применяется операция скалярного произведения векторов. Вот еще одна диаграмма, показывающая, как вычислить угол между двумя вершинами:
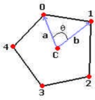
Нам нужно найти векторы a и b. Это можно сделать, вычтя центр c из вершин v0 и v1 соответственно. Затем полученные векторы a и b следует нормализовать. В формулах это записывается следующим образом:
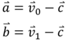
Скалярное произведение двух нормализованных векторов a и b, это число в диапазоне от –1 до +1. Значение –1 означает угол между векторами 180 градусов, 0 угол 90 градусов и +1 угол 0 градусов. Итак, чтобы найти угол A между нормализованными векторами a и b:
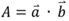
К сожалению, есть случай, когда этот способ не срабатывает. Чтобы устранить проблему, нужно отсеивать некоторые вершины, о них позже, а для начала я покажу вам проблемный случай:
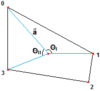
Когда уголOI > OII, вместо вершины 1 будет выбрана ошибочная вершина 3. Решение этой проблемы пропустить все вершины, находящиеся более чем на 180° от вектора a. Мы не можем сделать это с помощью операции векторного скалярного произведения, поскольку ее результат изменяется только от 0° до 180° (нам нужен полный диапазон 360°). Однако это можно сделать, создав плоскость по нормали полигона. Плоскость перпендикулярна плоскости полигона.
Все вершины, находящиеся за плоскостью можно пропустить. Точки, которые не будут пропущены, будут находиться в пределах от 0° до 180 ° от вектора a. Чтобы помочь вам визуализируем это:

Точки в серой области пропущены (на 2D виде), так как они находятся более чем на 180° от вектора a. Хотя я не уверен, но я думаю, что этот метод работает только для выпуклых полигонов. В псевдокоде весь этот алгоритм выглядит так:
Хотя вершины теперь отсортированы, они все еще могут быть расположены в неправильном порядке (против часовой стрелки). Причина в том, что этот код не учитывает то, как обращен полигон, то есть нормаль полигона. Если полигон обращен назад, то вершины расположены в неправильном порядке. Это можно проверить с помощью следующего псевдокода:
CalculateNormal вычислит нормаль для заданного набора вершин. ReverseVertexOrder обратит порядок данного набора вершин. Вы можете взглянуть на созданную мной функцию сортировки вершин по часовой стрелке. Она называется SortVerticesCW, и её можно найти в исходном коде. Если вы не знаете, как рассчитать нормаль полигона, ознакомьтесь с http://www.thecore.de/avgplane.pdf .
Выполнение конструктивного объединения твердотельной геометрии на всех брашах
Теперь, когда у нас есть правильные полигоны (с координатами текстуры) для каждого браша, нам нужно сгенерировать правильные полигоны. Чтобы получить правильные полигоны, необходимо выполнить объединение конструктивной твердотельной геометрии (CSG) для всех брашей в объекте. Взгляните на следующую диаграмму, чтобы понять, почему необходимо объединение CSG.
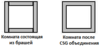
CSG объединение удалило все перекрывающиеся полигоны и полигоны, которые были внутри других брашей. Это не только уменьшает количество полигонов, но также генерирует геометрию, которую можно использовать для создания деревьев BSP. Большинство движков, использующих .MAP файлы для описания уровней, используют BSP деревья. Вот еще одна диаграмма, которая показывает результат CSG объединение.

Есть два широко распространенных алгоритма, которые выполняют операцию CSG с полигонами. Laidlaw подход выполняет операции CSG, используя только списки полигонов. Подход Naylor выполняет операции CSG с использованием деревьев BSP. Для каждой браша создается дерево BSP, которые затем накладываются друг на друга. Я выбрал подход Naylor и считаю, что это лучший подход в данной ситуации. Вы можете заметить, что следующий код очень похож на учебник «Удаление недопустимой геометрии из данных импортированных из Quake .MAP файлов », автор Gerald Filimonov известный по ником K9Megahertz (http://www.3dtechdev.com/tutorials/illegalgeometry/illegalgeometrytut.html). Мой код а также идеи базируются на основе его учебника. Возможно, вам будет полезно прочитать как его руководство, так и это.
Не волнуйтесь, если вы не знаете, как создавать деревья BSP, потому что в нашем случае они не нужны. Оба алгоритма CSG были разработаны для любых вогнутых или выпуклых многогранников. Однако наши браша представляют собой выпуклые многогранники. Это дает нам большое преимущество. Мы можем пропустить построение BSP-деревьев, потому что мы знаем, что, если точка находится перед любым из полигонов браша, она находится за пределами браша.
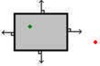
На диаграмме выше видно, что если точка находится перед любым из полигонов браша, то она находится снаружи браша. Если точка находится позади всех полигонов браша, она находится внутри браша. Это очень изящный трюк, теперь мы можем определить, находится ли какая-либо точка, линия или полигон внутри, снаружи или пересекает браш.
Псевдокод CSG объединения выглядит следующим образом:
Сначала необходимо сделать копию брашей, потому что одна копия используется для сопоставления с другой копией, чтобы определить, что нужно отсечь. Затем мы должны сопоставить с каждым брашем из второго массива все браши, кроме идентичных, из первого массива брашей и отсечь скрытые полигоны во втором массиве. Важно чтобы браши не сопоставлялись сами с собой, иначе отсекутся все полигоны браша. После того как мы сопоставили каждый браш с каждым, первый массив брашей больше не нужен. Второй массив брашей содержит все правильные полигоны. Одна вещь, которая может показаться неясной, - это то, что делает bClipOnPlane. bClipOnPlane - это флаг, который отслеживает, следует ли сохранить или удалить полигоны, лежащие в одной плоскости. Если бы каждый полигон в одной плоскости был сохранен, было бы несколько полигонов, покрывающих одну и ту же область. Если удалить все полигоны в одной плоскости, полигоны будут отсутствовать. В последующих функциях вы увидите, как используется bClipOnPlane.
Чтобы помочь вам визуализировать этот процесс, я нарисую схемы:
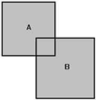
Два браша A и B будут сопоставлены друг с другом. Сделаны копии брашей A и B, это браши A' и B' соответственно. Сначала браш A' сопоставляется с брашем B.
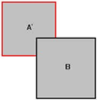
Затем браш B' сопоставляется с A.
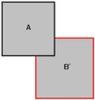
Поскольку брашей больше нет, сопоставление завершено. Если мы посмотрим на A 'и B', они объединены, а невидимые части отсечены.
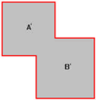
Взгляните еще раз на псевдокод, чтобы убедиться, что вы поняли, как это работает. Однако один вопрос остается открытым. Как работает ClipToBrush? ClipToBrush работает так:
Это упрощенная версия того, как объединить браш с другим брашем. Каждый полигон браша рассекается, сопоставляясь с каждым полигоном другого браша. Затем полученные полигоны (которые были рассечены) заменяются исходными полигонами. Я знаю, что это сбивает с толку, но потерпите немного. Я постараюсь визуализировать этот процесс. Мы отсекаем A' по B.
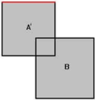
Первый полигон, который будет рассечён по брашу B, отмечен красным. Поскольку он находится за одним из полигонов B, после рассечения он должен быть за пределами браша B. Далее, мы переходим к следующему полигону в браше A'.
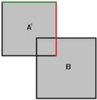
Полигоны, которые мы уже сопоставили и рассекли, отмечены зеленым. Сопоставляемый в настоящее время полигон красный. Этот полигон проходит через браш B. Его придётся рассечь. Возвращаются только рассечённые фрагменты вне браша B. В данном случае это только один фрагмент. Переходим к следующему полигону.
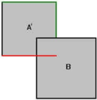
Вы уже должны начать понимать происходящее. Я перейду к следующему шагу без дальнейших объяснений.
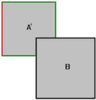
Снова у нас простой случай, когда полигон находится за пределами браша B. Мы закончили и браш A' был рассечён.
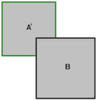
Следующий вопрос - как можно рассечь полигон сопоставив его со списком полигонов. Список полигонов - это набор выпуклых полигонов, образующих выпуклую оболочку (пересечение браша). В этом нам поможет рекурсивная функция, которая рассечёт полигон сопоставляя его со списком полигонов. Вот её псевдокод:
Функция начинается с классификации полигона, который может быть рассечён, относительно плоскости полигона, с которым он сопоставляется. Если полигон находится перед плоскостью, полигон будет возвращен без изменений, потому что он находится за пределами браша. Если полигон находится позади плоскости, он сопоставляется с оставшимися полигонами в списке. Однако если достигнут конец списка, это означает, что полигон находится внутри браша и его следует удалить.
Если полигон находится на плоскости, он сопоставляется с оставшимися полигонами в списке. Если достигнут конец списка, полигон можно удалить. Если нормаль полигона совпадает с нормалью плоскости и bClipOnPlane имеет значение false, то возвращается исходный полигон.
Если полигон пересекает другой полигон, его необходимо рассечь. Передний фрагмент определенно будет виден, но задний фрагмент необходимо сопоставить со следующими полигонами списка. Если достигнут конец списка, то возвращается только передний фрагмент, так как задний фрагмент находиться внутри браша. Если ни один задний фрагмент не возвращается после того, как он был сопоставлен с остальной части списка, это означает, что задний фрагмент находился внутри браша, и должен быть возвращен только передний фрагмент. Если задний фрагмент совпадает с полигонами, полученными при рассечении заднего фрагмента, то рассекать полигон нет необходимости.
Чтобы понять почему, рассмотрим этот случай:
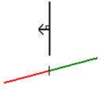
Рассечение полигона не имеет смысла, поскольку он не пересекает браш. Исходный полигон можно вернуть вместо разделения на переднюю и заднюю части. Это помогает свести количество полигонов к минимуму. Если конец списка не достигнут и задний фрагмент не равен фрагментам, возвращенным при отсечении заднего фрагмента, то необходимо вернуть передний и фрагменты, возвращенные при отсечении заднего фрагмента.
Я хотел бы упомянуть, что в псевдокоде я иногда обрабатывал списки полигонов как массивы, а иногда как связанные списки. Причина, по которой я сделал это, заключалась в том, чтобы сохранить простой псевдокод. В циклах for проще использовать массивы, в то время как легче добавить элемент в связанный список, чем повторно выделить массив для добавления элемента. Я бы рекомендовал вам использовать массивы для хранения списков полигонов из-за простоты. Однако вам нужно будет написать функции, которые будут иметь дело с добавлением полигонов в список. В исходном коде я использовал связанные списки. Однако их было труднее отлаживать, и это приводило к большему количеству кода (особенно в циклах for).
Чтобы по-настоящему понять алгоритм, я взял лист бумаги и применил алгоритм пошагово на простых случаях. Это действительно помогло мне понять, как это работает (особенно когда полигон находится на плоскости).
Классификация полигона относительно плоскости
Классификация полигона относительно плоскости - очень распространенная вещь. Вы хотите выяснить, находится ли полигон впереди, позади, на плоскости, рассекается плоскостью. Вот двухмерная иллюстрация этих четырех случаев:
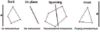
Случай, когда полигон находится на плоскости нарисовать сложно, но я, надеюсь, вам это понятно. Классификация положения полигона относительно плоскости довольно проста. Используя уравнение плоскости, , мы можем сопоставить любую точку с плоскостью. Если результат положительный, точка находится перед плоскостью. Если результат отрицательный, точка находится за плоскостью. Если результат равен нулю, то точка находится на плоскости. Псевдокод для классификации полигона относительно плоскости:
Разбиение полигона плоскостью
Если полигон пересекает плоскость, вы можете его разделить. При разбиении полигона плоскостью получается два фрагмента: передний и задний. Фронтальный фрагмент - это та часть полигона, которая находится перед плоскостью. Задний фрагмент - это та часть полигона, которая находится позади плоскости.
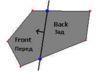
Мало того, что вершины должны быть назначены правильному фрагменту, ещё может потребоваться сгенерировать новые вершины для точек, где полигон пересекает плоскость. Они отмечены как большие синий точки на диаграмме выше. Чтобы создать новую вершину, в месте пересечения полигоном плоскости, нам нужно найти ребро, которым полигон пересекает плоскость. Мы можем рассматривать это ребро как отрезок прямой, который должен быть разделен плоскостью.
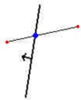
Чтобы вычислить новую вершину, мы сначала находим процент длины отрезка линии, на котором происходит пересечение:
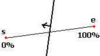
Формула для определения этого процента:
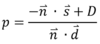
, где n и D - плоскость, s – первая вершина, а d - направление отрезка прямой. d можно вычислить путем вычитания e из s и нормализации результата. Обратите внимание: если знаменатель равен 0, то пересечения нет. p затем используется для вычисления новой вершины, v = s + pd. Если p используется для других вычислений (таких как вычисление новых координат текстуры) необходимо нормализовать p,
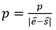
, где || обозначают магнитуду вектора.
Теперь вы знаете, как найти пересечение отрезка прямой с плоскостью. Пришло время показать вам код функции, которая разделит полигон плоскостью.
Исходный код
Исходные коды из этого документа, а также сам документ можно загрузить с моей домашней страницы по адресу http://www.uio.no/~stefanha. Исходный код - это мой полнофункциональный парсер .MAP. Он понимает .MAP файл, вычисляет полигоны для каждого браша, преобразует координаты в левую систему координат, масштабирует геометрию 128: 1, вычисляет координаты текстуры, выполняет объединение CSG для всех брашей каждого объекта и сохраняет объекты в файле .CMF. Я сам разработал формат файла .CMF. Это просто двоичный формат файла для хранения множества объектов. У каждого объекта могут быть свойства и полигоны. Причина, по которой я масштабирую геометрию, заключается в том, что я предпочитаю координаты с меньшими значениями.
Я также включил программу под названием CMFView, с помощью которой я отлаживал свою программу CSG. CMFView загружает файлы .CMF и отображает их. Однако я не могу гарантировать, что CMFView будет работать на всех ПК. Я также включил описание формата файла .CMF. Если хотите, можете использовать мою программу CSG вместо написания своей собственной. Чтобы скомпилировать .MAP файл, запустите консоль и введите «csg mapname.map mapname.cmf», где «mapname» - это имя вашей карты. Пожалуйста, прочтите файл readme перед использованием исходного кода или программ.
Специальная благодарность
Особая благодарность:
Ребятам с Mr. Game-Maker bulletin board. Telemachos, Gazza, Nitro, Proof, Magnus, и остальные (вы знаете, о ком я). Они помогли мне найти ошибки и многое мне объяснили.
Ники с Mr. Game-Maker bulletin board. Помог мне исправить ошибки с сортировкой вершин и показал, как вычислить средину плоскости полигона (http://www.thecore.de/avgplane.pdf ).
Джеральд Филимонов (он же K9Megahertz на Mr. Game-Maker bulletin board) обнаружил ошибки в псевдокоде сортировки вершин. Переход на его домашнюю страницу по адресу http://www.3dtechdev.com .
BlackFiend и MasterPoi (с Mr. Game-Maker bulletin board) обнаружили ошибки и помогли мне исправить их.
Шон Кавано из Gearbox Software. Он был первым, кто помог мне с доменом .MAP.файлы.
Люку Ходоровичу за ответы на мои вопросы. Посмотрите его проекты на http://gollum.flipcode.com .
Ян Бернье из Valve Software. Он показал мне, где вычисляются координаты текстуры в коде Half-Life.
Тай Мэтьюз, один из авторов Wally, за предоставленный мне код загрузки .WAD.
Библиография / Ссылки
Half-Life SDK (http://www.valvesoftware.com/hlsdk.htm )
Mr. Game-Maker bulletin board (http://www.mrgame-maker.com)
«Удаление недопустимой геометрии из данных, импортированных из Quake .MAP файлов», Джеральд Филимонов, он же K9Megahertz (http://www.3dtechdev.com/tutorials/illegalgeometry/illegalgeometrytut.html)
«Монтаж уровней» Люка Ходоровича (http://www.flipcode.com/tutorials/tut_levedit.shtml)
«Нахождение середины плоскости для набора точек» Ники (http://www.thecore.de/avgplane.pdf)
Далее я создам тему посвящённую этим статьям, где планирую выложить их в виде одного файла, а так же некоторые свои решения по оптимизации кода.
Сортировка вершин
Теперь у нас есть список допустимых полигонов с координатами текстуры для каждой вершины, мы уже довольно далеко продвинулись. Однако наши вершины расположены в более или менее случайном порядке. Чтобы воспользоваться преимуществами алгоритма отбраковки задних граней, вершины каждого полигона должны быть отсортированы либо по часовой стрелке, либо против часовой стрелки. Я предпочитаю сортировку по часовой стрелке, чтобы можно было отбраковывать полигоны с вершинами, расположенными против часовой стрелки. Описываемый мной метод также можно использовать с небольшими изменениями для сортировки вершин в порядке против часовой стрелки. Чтобы отсортировать вершины, нам нужна нормаль полигона. Но она у нас уже есть, и это нормаль грани, на плоскости которой лежит полигон.
Для начала нам нужно найти центр полигона. Это не что иное, как среднее значение всех его вершин. Псевдокод вычисления центра полигона:
Код:
Point center;
for n = 0 to NumberOfVertices – 1
{
center += vertices[ n ];
}
center /= NumberOfVertices;
Хотя это легко понять,но как мы можем сделать это математически? Для поиска угла между векторами применяется операция скалярного произведения векторов. Вот еще одна диаграмма, показывающая, как вычислить угол между двумя вершинами:

Нам нужно найти векторы a и b. Это можно сделать, вычтя центр c из вершин v0 и v1 соответственно. Затем полученные векторы a и b следует нормализовать. В формулах это записывается следующим образом:
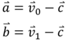
Скалярное произведение двух нормализованных векторов a и b, это число в диапазоне от –1 до +1. Значение –1 означает угол между векторами 180 градусов, 0 угол 90 градусов и +1 угол 0 градусов. Итак, чтобы найти угол A между нормализованными векторами a и b:
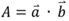
К сожалению, есть случай, когда этот способ не срабатывает. Чтобы устранить проблему, нужно отсеивать некоторые вершины, о них позже, а для начала я покажу вам проблемный случай:

Когда угол
Все вершины, находящиеся за плоскостью можно пропустить. Точки, которые не будут пропущены, будут находиться в пределах от 0° до 180 ° от вектора a. Чтобы помочь вам визуализируем это:

Точки в серой области пропущены (на 2D виде), так как они находятся более чем на 180° от вектора a. Хотя я не уверен, но я думаю, что этот метод работает только для выпуклых полигонов. В псевдокоде весь этот алгоритм выглядит так:
Код:
for n = 0 to NumberOfVertices – 3
{
Vector3 a = Normalize ( vertices[ n ] – center );
Plane p = PlaneFromPoints ( vertices[ n ], center, center + normal );
double SmallestAngle = -1;
int Smallest = -1;
for m = n + 1 to NumberOfVertices – 1
{
if ( p.ClassifyPoint ( vertices[ m ] ) != BACK )
{
Vector3 b = Normalize ( vertices[ m ] – center ); double Angle = a.Dot ( b );
if ( Angle > SmallestAngle )
{
SmallestAngle = Angle; Smallest = m;
}
}
}
swap ( vertices[ n + 1 ], vertices[ Smallest ] );
}
Код:
Normal n = CalculateNormal ( vertices );
if ( n.Dot ( normal ) < 0 )
{
ReverseVertexOrder ( vertices );
}Выполнение конструктивного объединения твердотельной геометрии на всех брашах
Теперь, когда у нас есть правильные полигоны (с координатами текстуры) для каждого браша, нам нужно сгенерировать правильные полигоны. Чтобы получить правильные полигоны, необходимо выполнить объединение конструктивной твердотельной геометрии (CSG) для всех брашей в объекте. Взгляните на следующую диаграмму, чтобы понять, почему необходимо объединение CSG.

CSG объединение удалило все перекрывающиеся полигоны и полигоны, которые были внутри других брашей. Это не только уменьшает количество полигонов, но также генерирует геометрию, которую можно использовать для создания деревьев BSP. Большинство движков, использующих .MAP файлы для описания уровней, используют BSP деревья. Вот еще одна диаграмма, которая показывает результат CSG объединение.

Есть два широко распространенных алгоритма, которые выполняют операцию CSG с полигонами. Laidlaw подход выполняет операции CSG, используя только списки полигонов. Подход Naylor выполняет операции CSG с использованием деревьев BSP. Для каждой браша создается дерево BSP, которые затем накладываются друг на друга. Я выбрал подход Naylor и считаю, что это лучший подход в данной ситуации. Вы можете заметить, что следующий код очень похож на учебник «Удаление недопустимой геометрии из данных импортированных из Quake .MAP файлов », автор Gerald Filimonov известный по ником K9Megahertz (http://www.3dtechdev.com/tutorials/illegalgeometry/illegalgeometrytut.html). Мой код а также идеи базируются на основе его учебника. Возможно, вам будет полезно прочитать как его руководство, так и это.
Не волнуйтесь, если вы не знаете, как создавать деревья BSP, потому что в нашем случае они не нужны. Оба алгоритма CSG были разработаны для любых вогнутых или выпуклых многогранников. Однако наши браша представляют собой выпуклые многогранники. Это дает нам большое преимущество. Мы можем пропустить построение BSP-деревьев, потому что мы знаем, что, если точка находится перед любым из полигонов браша, она находится за пределами браша.

На диаграмме выше видно, что если точка находится перед любым из полигонов браша, то она находится снаружи браша. Если точка находится позади всех полигонов браша, она находится внутри браша. Это очень изящный трюк, теперь мы можем определить, находится ли какая-либо точка, линия или полигон внутри, снаружи или пересекает браш.
Псевдокод CSG объединения выглядит следующим образом:
Код:
ClippedBrushes = CopyList ( ); // Копируем массив брашей
bool bClipOnPlane;
for i = 0 to NumberOfBrushes – 1
{
bClipOnPlane = false;
for j = 0 to NumberOfBrushes – 1
{
if ( i != j ) // Проверяем не сопоставляем ли мы браш с самим собой
{
}
else
{
ClippedBrushes[ i ].ClipToBrush ( Brushes[ j ], bClipOnPlane );
bClipOnPlane = true;
}
}
}
// Браши больше не нужны
return ClippedBrushes; // ClippedBrushes содержит все правильные полигоны
}Чтобы помочь вам визуализировать этот процесс, я нарисую схемы:

Два браша A и B будут сопоставлены друг с другом. Сделаны копии брашей A и B, это браши A' и B' соответственно. Сначала браш A' сопоставляется с брашем B.

Затем браш B' сопоставляется с A.

Поскольку брашей больше нет, сопоставление завершено. Если мы посмотрим на A 'и B', они объединены, а невидимые части отсечены.

Взгляните еще раз на псевдокод, чтобы убедиться, что вы поняли, как это работает. Однако один вопрос остается открытым. Как работает ClipToBrush? ClipToBrush работает так:
Код:
void Brush::ClipToBrush ( Brush *pBrush, bool bClipOnPlane )
{
for i = 0 to NumberOfPolygons – 1
{
Polygons[ i ] = Polygons[ i ].ClipToList ( pBrush.Polygons, bClipOnPlane );
}
}
Первый полигон, который будет рассечён по брашу B, отмечен красным. Поскольку он находится за одним из полигонов B, после рассечения он должен быть за пределами браша B. Далее, мы переходим к следующему полигону в браше A'.

Полигоны, которые мы уже сопоставили и рассекли, отмечены зеленым. Сопоставляемый в настоящее время полигон красный. Этот полигон проходит через браш B. Его придётся рассечь. Возвращаются только рассечённые фрагменты вне браша B. В данном случае это только один фрагмент. Переходим к следующему полигону.

Вы уже должны начать понимать происходящее. Я перейду к следующему шагу без дальнейших объяснений.

Снова у нас простой случай, когда полигон находится за пределами браша B. Мы закончили и браш A' был рассечён.

Следующий вопрос - как можно рассечь полигон сопоставив его со списком полигонов. Список полигонов - это набор выпуклых полигонов, образующих выпуклую оболочку (пересечение браша). В этом нам поможет рекурсивная функция, которая рассечёт полигон сопоставляя его со списком полигонов. Вот её псевдокод:
Код:
Polygon *Polygon::ClipToList ( Polygon * polygon, bool bClipOnPlane )
{
switch ( ClassifyPolygon ( polygon ) )
{
case FRONT: // Полигон находится вне браша возвращаем его
return polygon;
case BACK:
if ( IsLast ( ) ) // Полигон находится внутри браша
{
return NULL;
}
return pNext->ClipToList ( polygon, bClipOnPlane );
case ONPLANE:
double Angle = polygon.normal.Dot ( normal ) – 1;
if ( ( Angle > -epsilon ) && ( Angle < epsilon ) )
{
if ( !bClipOnPlane )
{
return polygon;
}
}
if ( IsLast ( ) )
{
return NULL;
}
return pNext->ClipToList ( polygon, bClipOnPlane );
case SPANNING:
SplitPoly ( polygon, front, back ); // Рассекаем полигон на два фрагмента
if ( IsLast ( ) ) // Задний фрагмент находится внутри браша, поэтому возвращаем только передний
{
return front;
}
BackFrags = pNext->ClipToList ( back, bClipOnPlane ); // Сопоставляем задний фрагмент, чтобы проверить
// не осталось ли видимых участков
If ( BackFrags == NULL )
{
return front;
}
if ( BackFrags == back ) // Не требуется рассекать полигон, так как он целиком находится перед брашем {
return polygon;
}
front.AddPolygon ( BackFrags ); // Добавляем задний фрагмент в список передних
return front;
}
}Если полигон находится на плоскости, он сопоставляется с оставшимися полигонами в списке. Если достигнут конец списка, полигон можно удалить. Если нормаль полигона совпадает с нормалью плоскости и bClipOnPlane имеет значение false, то возвращается исходный полигон.
Если полигон пересекает другой полигон, его необходимо рассечь. Передний фрагмент определенно будет виден, но задний фрагмент необходимо сопоставить со следующими полигонами списка. Если достигнут конец списка, то возвращается только передний фрагмент, так как задний фрагмент находиться внутри браша. Если ни один задний фрагмент не возвращается после того, как он был сопоставлен с остальной части списка, это означает, что задний фрагмент находился внутри браша, и должен быть возвращен только передний фрагмент. Если задний фрагмент совпадает с полигонами, полученными при рассечении заднего фрагмента, то рассекать полигон нет необходимости.
Чтобы понять почему, рассмотрим этот случай:

Рассечение полигона не имеет смысла, поскольку он не пересекает браш. Исходный полигон можно вернуть вместо разделения на переднюю и заднюю части. Это помогает свести количество полигонов к минимуму. Если конец списка не достигнут и задний фрагмент не равен фрагментам, возвращенным при отсечении заднего фрагмента, то необходимо вернуть передний и фрагменты, возвращенные при отсечении заднего фрагмента.
Я хотел бы упомянуть, что в псевдокоде я иногда обрабатывал списки полигонов как массивы, а иногда как связанные списки. Причина, по которой я сделал это, заключалась в том, чтобы сохранить простой псевдокод. В циклах for проще использовать массивы, в то время как легче добавить элемент в связанный список, чем повторно выделить массив для добавления элемента. Я бы рекомендовал вам использовать массивы для хранения списков полигонов из-за простоты. Однако вам нужно будет написать функции, которые будут иметь дело с добавлением полигонов в список. В исходном коде я использовал связанные списки. Однако их было труднее отлаживать, и это приводило к большему количеству кода (особенно в циклах for).
Чтобы по-настоящему понять алгоритм, я взял лист бумаги и применил алгоритм пошагово на простых случаях. Это действительно помогло мне понять, как это работает (особенно когда полигон находится на плоскости).
Классификация полигона относительно плоскости
Классификация полигона относительно плоскости - очень распространенная вещь. Вы хотите выяснить, находится ли полигон впереди, позади, на плоскости, рассекается плоскостью. Вот двухмерная иллюстрация этих четырех случаев:

Случай, когда полигон находится на плоскости нарисовать сложно, но я, надеюсь, вам это понятно. Классификация положения полигона относительно плоскости довольно проста. Используя уравнение плоскости, , мы можем сопоставить любую точку с плоскостью. Если результат положительный, точка находится перед плоскостью. Если результат отрицательный, точка находится за плоскостью. Если результат равен нулю, то точка находится на плоскости. Псевдокод для классификации полигона относительно плоскости:
Код:
int iFront, iBack, iOnPlane;
for n = 0 to NumberOfVertices – 1
{
double result = n.Dot ( vertices[ n ] ) + d;
if ( result > 0 )
{
iFront++;
}
else if ( result < 0 )
{
}
else
{
}
iBack++;
iOnPlane++;
}
if ( iFront == NumberOfVertices )
{
return FRONT;
}
if ( iBack == NumberOfVertices )
{
return BACK;
}
if ( iOnPlane == NumberOfVertices )
{
return ONPLANE;
}
return SPANNING;Если полигон пересекает плоскость, вы можете его разделить. При разбиении полигона плоскостью получается два фрагмента: передний и задний. Фронтальный фрагмент - это та часть полигона, которая находится перед плоскостью. Задний фрагмент - это та часть полигона, которая находится позади плоскости.

Мало того, что вершины должны быть назначены правильному фрагменту, ещё может потребоваться сгенерировать новые вершины для точек, где полигон пересекает плоскость. Они отмечены как большие синий точки на диаграмме выше. Чтобы создать новую вершину, в месте пересечения полигоном плоскости, нам нужно найти ребро, которым полигон пересекает плоскость. Мы можем рассматривать это ребро как отрезок прямой, который должен быть разделен плоскостью.

Чтобы вычислить новую вершину, мы сначала находим процент длины отрезка линии, на котором происходит пересечение:

Формула для определения этого процента:
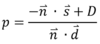
, где n и D - плоскость, s – первая вершина, а d - направление отрезка прямой. d можно вычислить путем вычитания e из s и нормализации результата. Обратите внимание: если знаменатель равен 0, то пересечения нет. p затем используется для вычисления новой вершины, v = s + pd. Если p используется для других вычислений (таких как вычисление новых координат текстуры) необходимо нормализовать p,
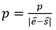
, где || обозначают магнитуду вектора.
Теперь вы знаете, как найти пересечение отрезка прямой с плоскостью. Пришло время показать вам код функции, которая разделит полигон плоскостью.
Код:
void SplitPolygon ( Polygon* pPoly_, Plane* pPlane_, Polygon* pFront_, Polygon* pBack_ )
{
//
// Классифицируем все вершины
//
Classify Positions[ NumberOfVertices ];
for n = 0 to NumberOfVertices – 1
{
Positions[ n ] = pPlane_->ClassifyPoint ( pPoly_->vertices[ n ] );
}
//
// Строим передний и задний фрагменты
//
for n = 0 to NumberOfVertices – 1
{
int m = n + 1;
bool bIgnore = false ;
if ( n == NumberOfVertices – 1 )
{
m = 0;
}
switch ( Positions[ n ] )
{
case FRONT:
pFront->AddVertex ( pPoly_->vertices[ n ] );
case BACK:
pBack->AddVertex ( pPoly_->vertices[ n ] );
case ONPLANE:
pFront->AddVertex ( pPoly_->vertices[ n ] );
pBack->AddVertex ( pPoly_->vertices[ n ] );
}
if ( ( Positions[ n ] == ONPLANE ) && ( Positions[ m ] != ONPLANE ) )
{
bIgnore = true;
}
else if ( ( Positions[ m ] == ONPLANE ) && ( Positions[ n ] != ONPLANE ) )
{
bIgnore = true;
}
if ( ( !bIgnore ) && ( Positions[ n ] != Positions[ m ] ) )
{
//
// Вычисляем новую вершину
//
Vector3 d = ( pPoly_->vertices[ n ] – pPoly->vertices[ m ] ).Normalize ( );
double denom = pPlane_->n.Dot ( d );
if ( denom == 0 )
{
continue;
}
double p = -( pPlane_->n.Dot ( pPoly_->vertices[ n ] ) + pPlane_->d ) ) / denom;
Vertex v = pPoly_->vertices[ n ] + ( p * d ) ;
p = p / ( End – Start ).Magnitude ( ) ;
//
// Вычисляем новые текстурные координаты вершин
//
double du = pPoly_->vertices[ m ].tu - pPoly_->vertices[ n ].tu ;
double dv = pPoly_->vertices[ m ].tv - pPoly_->vertices[ n ].tv ;
du = du / sqrt ( du * du + dv * dv );
dv = dv / sqrt( du * du + dv * dv ) ;
v.tu = pPoly_->vertices[ n ].tu + ( p * du );
v.tv = pPoly_->vertices[ n ].tv + ( p * dv );
//
// Добавляем вершины к фрагменту
//
pFront_->AddVertex ( v ); pBack_->AddVertex ( v );
}
}
}Исходные коды из этого документа, а также сам документ можно загрузить с моей домашней страницы по адресу http://www.uio.no/~stefanha. Исходный код - это мой полнофункциональный парсер .MAP. Он понимает .MAP файл, вычисляет полигоны для каждого браша, преобразует координаты в левую систему координат, масштабирует геометрию 128: 1, вычисляет координаты текстуры, выполняет объединение CSG для всех брашей каждого объекта и сохраняет объекты в файле .CMF. Я сам разработал формат файла .CMF. Это просто двоичный формат файла для хранения множества объектов. У каждого объекта могут быть свойства и полигоны. Причина, по которой я масштабирую геометрию, заключается в том, что я предпочитаю координаты с меньшими значениями.
Я также включил программу под названием CMFView, с помощью которой я отлаживал свою программу CSG. CMFView загружает файлы .CMF и отображает их. Однако я не могу гарантировать, что CMFView будет работать на всех ПК. Я также включил описание формата файла .CMF. Если хотите, можете использовать мою программу CSG вместо написания своей собственной. Чтобы скомпилировать .MAP файл, запустите консоль и введите «csg mapname.map mapname.cmf», где «mapname» - это имя вашей карты. Пожалуйста, прочтите файл readme перед использованием исходного кода или программ.
Специальная благодарность
Особая благодарность:
Ребятам с Mr. Game-Maker bulletin board. Telemachos, Gazza, Nitro, Proof, Magnus, и остальные (вы знаете, о ком я). Они помогли мне найти ошибки и многое мне объяснили.
Ники с Mr. Game-Maker bulletin board. Помог мне исправить ошибки с сортировкой вершин и показал, как вычислить средину плоскости полигона (http://www.thecore.de/avgplane.pdf ).
Джеральд Филимонов (он же K9Megahertz на Mr. Game-Maker bulletin board) обнаружил ошибки в псевдокоде сортировки вершин. Переход на его домашнюю страницу по адресу http://www.3dtechdev.com .
BlackFiend и MasterPoi (с Mr. Game-Maker bulletin board) обнаружили ошибки и помогли мне исправить их.
Шон Кавано из Gearbox Software. Он был первым, кто помог мне с доменом .MAP.файлы.
Люку Ходоровичу за ответы на мои вопросы. Посмотрите его проекты на http://gollum.flipcode.com .
Ян Бернье из Valve Software. Он показал мне, где вычисляются координаты текстуры в коде Half-Life.
Тай Мэтьюз, один из авторов Wally, за предоставленный мне код загрузки .WAD.
Библиография / Ссылки
Half-Life SDK (http://www.valvesoftware.com/hlsdk.htm )
Mr. Game-Maker bulletin board (http://www.mrgame-maker.com)
«Удаление недопустимой геометрии из данных, импортированных из Quake .MAP файлов», Джеральд Филимонов, он же K9Megahertz (http://www.3dtechdev.com/tutorials/illegalgeometry/illegalgeometrytut.html)
«Монтаж уровней» Люка Ходоровича (http://www.flipcode.com/tutorials/tut_levedit.shtml)
«Нахождение середины плоскости для набора точек» Ники (http://www.thecore.de/avgplane.pdf)
Последнее редактирование: